L'IA dans les jeux vidéo - Partie 3
Comme nous l’avons vu dans les articles précédents, l’IA dans les jeux vidéo est principalement utilisée pour implémenter les comportements des personnages non joueurs. Cette approche a eu tellement d’importance que d’autres problématiques potentiellement adressées par l’IA ont longtemps été négligées. Récemment, ce genre d’approche alternative a commencé à se développer de plus en plus, la principale étant probablement la génération procédurale de contenu.
La génération procédurale
La génération procédurale de contenu fait référence aux méthodes qui permettent de générer du contenu dans un jeu avec peu ou pas d’intervention humaine. Le contenu généré peut être de nature très variée et toucher à presque l’intégralité d’un jeu. On peut citer : des niveaux, des terrains, des règles de jeux, des textures, des histoires, des objets, des quêtes, des armes, des musiques, des véhicules, des personnes,.. En général, on considère que le comportement des PNJs ainsi que le moteur du jeu ne correspondent pas à du contenu à proprement parler. L’utilisation la plus fréquente de génération procédurale est probablement la création de niveaux et de terrains.
L’utilisation de la génération procédurale a explosé depuis le milieu des années 2000 cependant le domaine existe depuis très longtemps. En effet, en 1980 le jeu Rogue utilisait déjà de la génération procédurale pour créer automatiquement ses niveaux et placer les objets dans ceux-ci. En 1984, Elite un jeu de simulation de commerce spatial générait quant à lui de nouveaux systèmes planétaires (avec leur économie, politique et population) durant le jeu.
Les objectifs
Quel est l’intérêt de la génération procédurale ? Les premiers jeux ont utilisé la génération procédurale pour permettre de réduire l’espace de stockage. En effet, en générant à la volée les textures et les niveaux du jeu, il n’est plus nécessaire de les stocker sur la cartouche ou autres médium du jeu. Cela permettait de dépasser les limites physiques imposées par les technologies de l’époque et donc de faire des jeux potentiellement beaucoup plus grands. Par exemple Elite présentait plusieurs centaines de systèmes planétaires en ne nécessitant seulement que de quelques dizaines de kilooctets (ko) sur la machine.
À l’heure actuelle cela n’est plus la principale raison d’utiliser la génération procédurale. Elle permet surtout de générer de grandes quantités de contenu sans devoir tout concevoir à la main. Dans le développement d’un jeu, la phase de création du contenu peut être très lourde et prendre une part importante du budget. La génération procédurale peut permettre d’accélérer la création de ce contenu.

Anastasia Opara (SEED - Search for Extraordinary Experiences Division - chez Electronic Arts) présente dans cette conférence sa vision de la génération de contenu. La création de contenu présente pour elle une phase de créativité qui correspond à la recherche de l’idée et de création artistique puis une phase de fabrication et d’implémentation de cette idée dans le jeu vidéo. Elle présente cette phase comme une montagne nécessitant des compétences particulières et un investissement en temps très important pour être franchie. La génération procédurale de contenu peut être une approche pour tenter de réduire la taille de cette montagne et permettre ainsi aux artistes de se concentrer principalement sur la créativité pure en s’abstrayant de la difficulté d’implémentation.
En plus de faciliter la phase de fabrication du contenu, la génération procédurale peut aussi encourager la créativité des artistes en proposant du contenu inattendu et intéressant. La génération procédurale présente ainsi un aspect de collaboration entre l’artiste et la machine. On peut ainsi trouver des galeries d’oeuvres d’art générées procéduralement.

La génération procédurale de contenu pourrait ainsi favoriser la création humaine et permettre la création de nouvelles expériences de jeu et même potentiellement de nouveaux genres de jeu. On pourrait ainsi imaginer possible une personnalisation des jeux bien plus poussée que ce qui existe actuellement en modifiant le contenu du jeu dynamiquement en fonction des interactions avec le joueur.
Enfin, avec une génération procédurale capable de produire du contenu en variété, qualité et quantité suffisante, il semble possible de créer des jeux qui ne finissent jamais et donc avec une rejouabilité ultime. Cependant, comme les développeurs s’en sont rendu compte (notamment ceux de No Man’s Sky), la quantité de contenu dans un jeu ne rend pas celui-ci forcément intéressant. Il y a donc un compromis vital à trouver entre la quantité de contenu que l’on génère et la qualité de celui-ci (intéressant, varié, etc..). Par exemple dans le jeu Elite présenté précédemment, les concepteurs prévoyaient de générer 282 billions de galaxies (c’est beaucoup). L’éditeur du jeu les a convaincus de se limiter à 8 galaxies, chacune composée de 256 étoiles. Avec ce nombre plus mesuré d’étoiles à créer, le générateur du jeu a pu rendre chaque étoile relativement unique, ce qui aurait été impossible avec le nombre de galaxies prévu initialement. Ainsi, le jeu proposait un bon équilibre entre taille, densité et variabilité. Avec la génération procédurale de contenu, on peut vite tomber dans le piège d’un univers gigantesque où absolument tout se ressemble. Chaque élément sera mathématiquement différent mais du point de vue du joueur, une fois qu’il a vu une étoile, il les a toutes vues.
Il y a donc en général un équilibre à trouver entre la taille du monde, sa diversité et le temps alloué du développeur. Générer le contenu à travers les mathématiques est la partie scientifique, alors que trouver le bon équilibre entre les différents éléments correspond à la partie artistique.
Les différentes approches
Il y a énormément d’approches pour faire de la génération procédurale de contenu et toutes ne sont pas basées sur de l’intelligence Artificielle. Des méthodes souvent simples sont utilisées à l’instar de la conception des comportements des PNJs afin de pouvoir garder un contrôle plus facilement sur le rendu final. En effet, le contenu généré doit respecter certaines contraintes afin d’être bien intégré dans le jeu.
Nous allons donc d’abord nous intéresser aux principales méthodes classiques de génération procédurale, puis nous ferons un tour d’horizon (non exhaustif) des approches basées sur l’IA.
La génération procédurale constructive
Les approches basées sur des tuiles
La méthode la plus simple et la plus fréquemment utilisée est la méthode basée sur des tuiles. L’idée est simple : le monde du jeu est découpé en sous parties (les tuiles), par exemple des salles dans un jeu d’exploration de donjon. Un grand nombre de salles sont modélisées à la main. Lors de la génération du monde, on sélectionne aléatoirement les salles pré-modélisées pour créer un univers plus grand. Si un assez grand nombre de tuiles ont été définies en amont, par la magie de la combinatoire, on peut obtenir un générateur de monde qui ne produira quasiment jamais deux fois le même résultat.

Spelunky génère procéduralement ses niveaux
En général, ce type d’approche implémente aussi des règles métiers spécifiques qui permettent d’assurer que le résultat sera jouable et intéressant. Par exemple dans un jeu d’exploration comme Spelunky, le générateur s’assure de choisir des tuiles de façon à construire un chemin viable pour le joueur puis remplit les espaces restants avec des tuiles aléatoires. Il peut ensuite parfois nécessiter quelques retraitements entre les tuiles si celles-ci ne s’imbriquent pas correctement les unes aux autres.
Cette approche est souvent utilisée pour générer le terrain ou le monde dans des jeux de type Rogue-like (Cette catégorie de jeu tire son nom du jeu Rogue de 1980 présenté précédemment. On peut citer notamment la série Diablo, The Binding of Isaac, Spelunky ou Rogue Legacy) mais elle permet aussi de générer bien d’autres types d’éléments et d’objets. Par exemple, dans le jeu Borderlands, les armes sont générées par un système basé sur des tuiles.

Différentes tuiles d’une arme dans Borderlands
Les armes sont découpées en sous parties qui sont interchangeables. Chaque arme générée est un tirage aléatoire des différentes sous-parties. Chacune de celles-ci a des répercussions sur les statistiques de l’arme comme le temps de chargement, le type de munition, la précision etc.. ce qui fait que toutes les armes générées sont légèrement différentes les unes des autres.
Les approches fractales
Les approches fractales tirent leur nom des célèbres objets mathématiques puisqu’elles ont quelques propriétés similaires. En effet, ces approches de génération procédurale sont basées sur des systèmes de couches successives à différentes échelles, un peu comme des fractales.

Le triangle de Sierpiński est une fractale
On va voir deux types d’approches fractales : les méthodes basées sur le bruit et les méthodes basées sur des grammaires.
Méthodes basées sur le bruit
Lorsque l’on observe le monde depuis un avion, l’agencement du terrain semble être relativement aléatoire. L’idée des approches basées sur le bruit est de se baser sur de l’aléatoire pour générer des terrains s’approchant de ceux du monde réel.
Lorsque l’on tire aléatoirement une séquence de valeurs, on obtient ce qu’on appelle du bruit blanc.
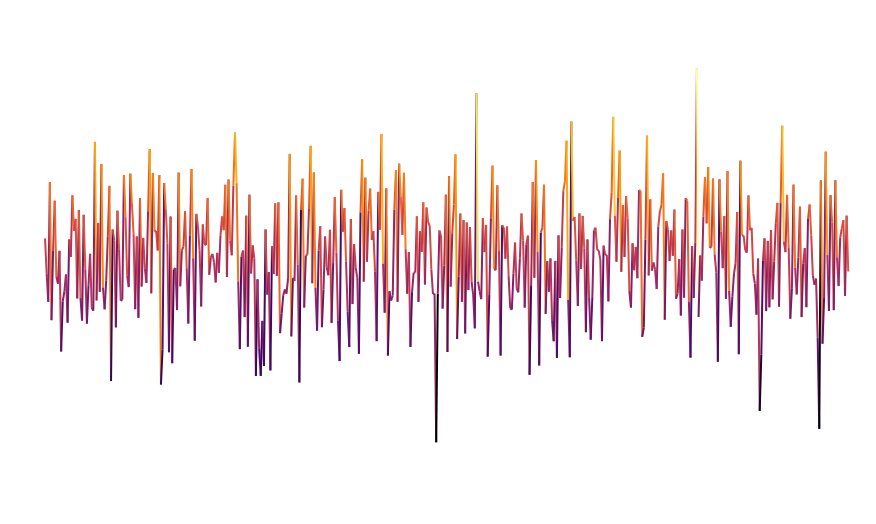
Bruit blanc en une dimension
Le bruit blanc n’est pas d’une grande aide pour la génération procédurale puisqu’il est la représentation d’un processus complètement aléatoire (ce qui n’est clairement pas le cas de notre monde). Cependant, il existe d’autres types de bruit qui représentent de l’aléatoire tout en conservant une structure locale. Le plus connu dans le cadre de la génération procédurale est probablement le bruit de Perlin. Ce bruit est généré par un processus aléatoire, cependant les points proches ne sont plus indépendants les uns des autres comme pour du bruit blanc. Cela permet d’obtenir des courbes comme celle ci-dessous qui sont plus lisses localement.
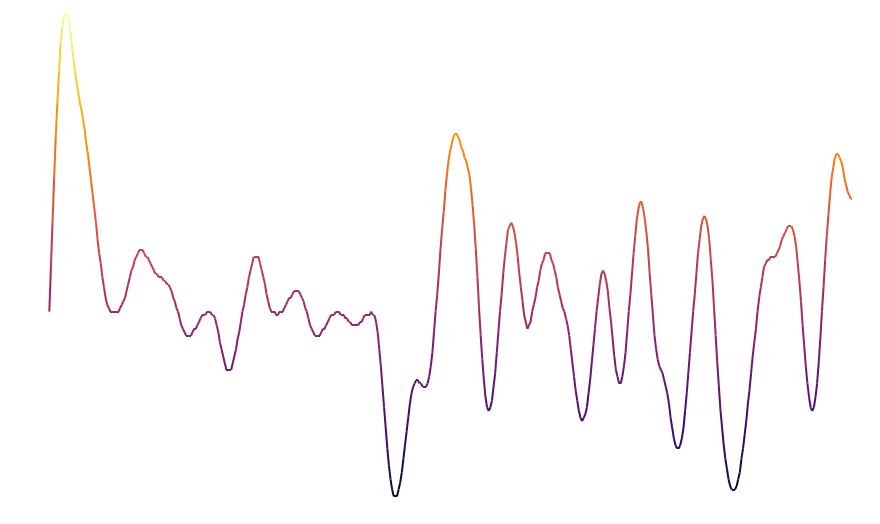
Bruit de perlin en une dimension
Les algorithmes basés sur le bruit deviennent intéressants surtout lorsqu’on augmente le nombre de dimensions. Ainsi, si on prend une grille en deux dimensions et que l’on fait un tirage de bruit blanc et de bruit de Perlin, on obtient les résultats suivants.
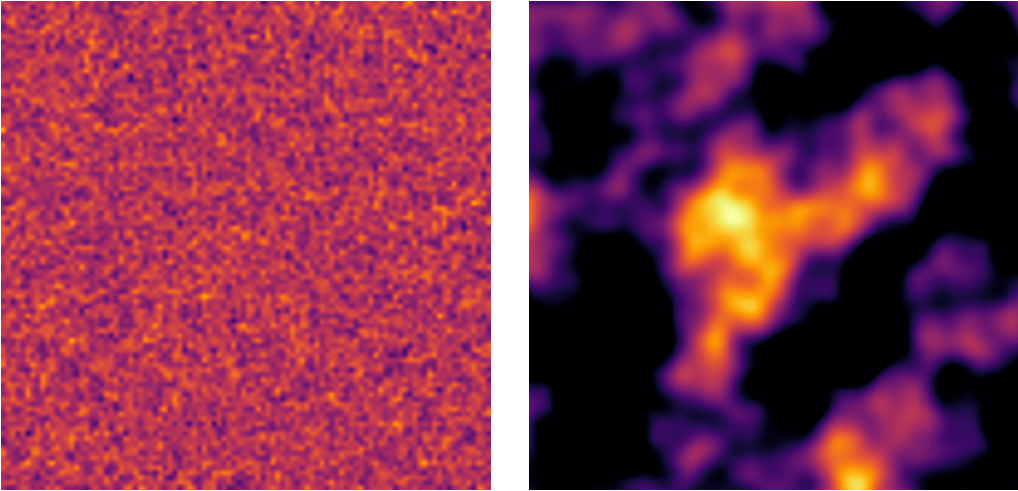
Bruit blanc (à gauche) et bruit de Perlin (à droite). Chaque pixel est coloré en fonction de sa valeur.
On obtient ainsi pour chaque pixel de la grille une valeur. On peut ensuite considérer la valeur de ce pixel comme une altitude et d’afficher la grille en 3 dimensions. On obtient ainsi une représentation d’un terrain montagneux, intégralement généré par du bruit de Perlin.

La grille de perlin générée précédemment affichée en 3 dimensions
Le problème du bruit de Perlin est qu’il va avoir tendance à générer des éléments répétitifs et de tailles relativement similaires. On risque ainsi d’obtenir un monde montagneux mais très vide, sans aucun détail entre les montagnes.
Pour éviter ce problème, on utilise plusieurs couches de bruit de Perlin à différentes échelles (on parle d’octaves). Ainsi la première couche sert à générer la géographie grosse-maille du monde et les couches suivantes ajoutent successivement des niveaux de détails de plus en plus fins. On retrouve ainsi l’idée des fractales.
Le bruit de Perlin est probablement l’approche la plus utilisé pour la génération procédurale puisque la génération de terrain est un besoin récurrent dans les jeux vidéo. Cette approche est notamment utilisée par Minecraft pour générer ses mondes.

Un monde de minecraft généré procéduralement
De nombreuses variations existent autour du bruit de Perlin, puisqu’il faut souvent l’adapter aux besoins spécifiques de chaque jeu. On peut citer le Simplex noise qui est une amélioration du bruit de Perlin (proposée par l’inventeur du bruit de Perlin - Ken Perlin - lui-même). Dans le jeu No man’s sky où presque tout l’univers est généré procéduralement, les planètes sont basées sur ce que les concepteurs appellent l’”Uber noise” qui est une approche se basant sur le bruit de Perlin et combinant nombreux autres types de bruits. Leur approche est censée donner des résultats plus réalistes (et donc plus intéressants pour le joueur) que celles basées seulement sur du bruit de Perlin.
Approches basées sur des grammaires
Une grammaire formelle peut être définie comme un ensemble de règles qui s’appliquent sur du texte. Les règles de la grammaire permettent de transformer une chaine de caractère en une autre. Par exemple :
A -> AB
B -> A
Avec la 1ère règle à chaque fois qu’il y aura un “A” dans une chaîne de caractère il sera transformé en “AB” et avec la deuxième règle un “B” sera transformé en “A”.
Les grammaires formelles ont de nombreuses applications en informatique et en IA, mais nous allons nous intéresser à un type de grammaire particulier appelé L-systèmes. Les L-systèmes ont la particularité d’être des grammaires pensées pour faire de la génération de plantes. Les L-systèmes présentent des règles récursives, ce qui rend facile la génération de formes fractales. Dans la nature de nombreuses plantes présentent des formes fractales, le chou romanesco étant l’un des exemples les plus frappants

Un chou romanesco
Un L-système est défini par un alphabet, un ensemble de règles, des modifications et un axiome de départ (qui est la chaîne de caractère que l’on considère pour démarrer)
Prenons un exemple simple :
Un alphabet restreint : {A,B}
Deux simples règles :
1. A → AB
2. B → A
L’axiome de départ : A
L’idée est d’appliquer plusieurs fois les règles au résultat obtenu précédemment (n étant le nombre de fois où la règle à été appliquée).
On obtient les résultats suivants:
n = 0 -> A
n = 1 -> AB
n = 2 -> ABA
n = 3 -> ABAAB
n = 4 -> ABAABABA
n = 5 -> ABAABABAABAAB
n = 6 -> ABAABABAABAABABAABABA
n = 7 -> ABAABABAABAABABAABABAABAABABAABAAB
On peut se demander où est le lien entre cette génération de chaîne de caractère et les plantes. L’idée est d’associer à chaque caractère de l’alphabet une action de dessin. Les chaînes de caractères générées vont donc être des sortes de plans de dessins.
Par exemple on peut considérer un L-système avec l’alphabet suivant:
- F : tracer un trait d’une certaine longueur (par ex 10 pixels)
- + : tourner à gauche de 30 degrés
- - : tourner à droite de 30 degrés
- [ : garder en mémoire la position et orientation actuelle
- ] : revenir à la position et l’orientation en mémoire
On définit une seule règle dans la grammaire :
F → F[−F]F[+F][F]
L’axiome de départ est : F
Ainsi, pour les différentes itérations, on obtient les résultats suivants. (Les couleurs permettent de faire le lien entre les chaînes de caractères générées et les dessins équivalents)
n = 0 -> F
n = 1 -> F [-F] F [+F] F
n = 2 -> F[−F]F[+F][F] [-F[−F]F[+F][F]] F[−F]F[+F][F] [+F[−F]F[+F][F]] [F[−F]F[+F][F]]
n = 3 -> F[−F]F[+F][F] [-F[−F]F[+F][F]] F[−F]F[+F][F] [+F[−F]F[+F][F]] [ F[−F]F[+F][F]] [−F[−F]F[+F][F] [-F[−F]F[+F][F]] F[−F]F[+F][F] [+F[−F]F[+F][F]] [ F[−F]F[+F][F]]] F[−F]F[+F][F] [-F[−F]F[+F][F]] F[−F]F[+F][F] [+F[−F]F[+F][F]] [ F[−F]F[+F][F]] [F[−F]F[+F][F] [-F[−F]F[+F][F]] F[−F]F[+F][F] [+F[−F]F[+F][F]] [F[−F]F[+F][F]]] [F[−F]F[+F][F] [-F[−F]F[+F][F]] F[−F]F[+F][F] [+F[−F]F[+F][F]] [ F[−F]F[+F][F]]]

Résultats obtenus en dessinant les chaînes des caractères après plusieures d’itérations
On peut ainsi continuer à appliquer la règle jusqu’à obtenir un résultat satisfaisant. Les résultats obtenus avec cette grammaire peuvent paraître simplistes mais avec les bonnes règles de grammaire et en itérant l’algorithme assez longtemps, on peut obtenir des résultats très convaincant comme ceux présentés ci-dessous. Il suffit ensuite d’ajouter des textures et des feuilles pour obtenir une belle végétation.
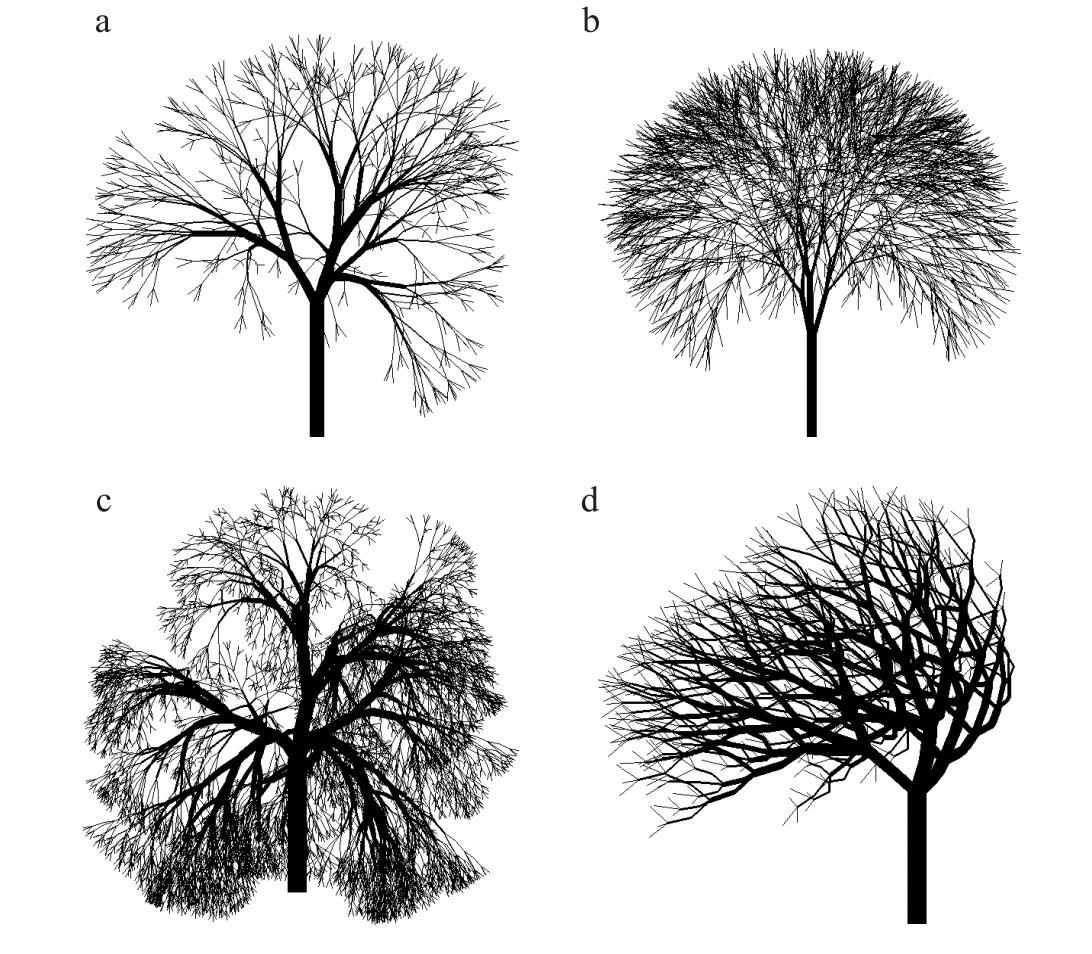
Résultats obtenus avec des L-systèmes plus poussés
Les L-systèmes ont l’avantage d’être très simple à définir en théorie (une seule règle de grammaire peut être suffisante). En pratique cependant, les choses ne sont pas si simples. En effet, les liens entre axiomes, règles et résultats sous forme de dessins après expansions sont très complexes. Il est donc difficile de prévoir le résultat en amont et le tâtonnement semble nécessaire. Ce site permet de jouer avec des L-systèmes afin de visualiser les résultats de grammaire prédéfinies, ainsi que de modifier les règles de ces grammaires et voir l’impact sur les résultats.
Un autre désavantage est que les L-systèmes sont limités à la génération de formes géométriques qui ont des propriétés fractales. C’est pourquoi ils sont principalement utilisés pour la génération de plantes. Il existe cependant de nombreuses extensions au principe basique des L-système, comme des systèmes avec de l’aléatoire ou des systèmes prenant en compte le contexte. Ces extensions permettent de produire du contenu plus varié. Ainsi, les L-systèmes ont parfois été utilisés pour générer des donjons, des rochers ou encore des caves.

Lien entre L-système et triangle de Sierpiński
L’image présentée plus tôt dans l’article avec un arbre de nuit a été générée par un système de grammaire (plus complet que celui présenté ici). Ce lien présente les règles utilisées pour générer l’image. Les résultats obtenus par ces méthodes peuvent être superbes. En modifiant légèrement les règles de grammaire, on peut générer des images différentes.
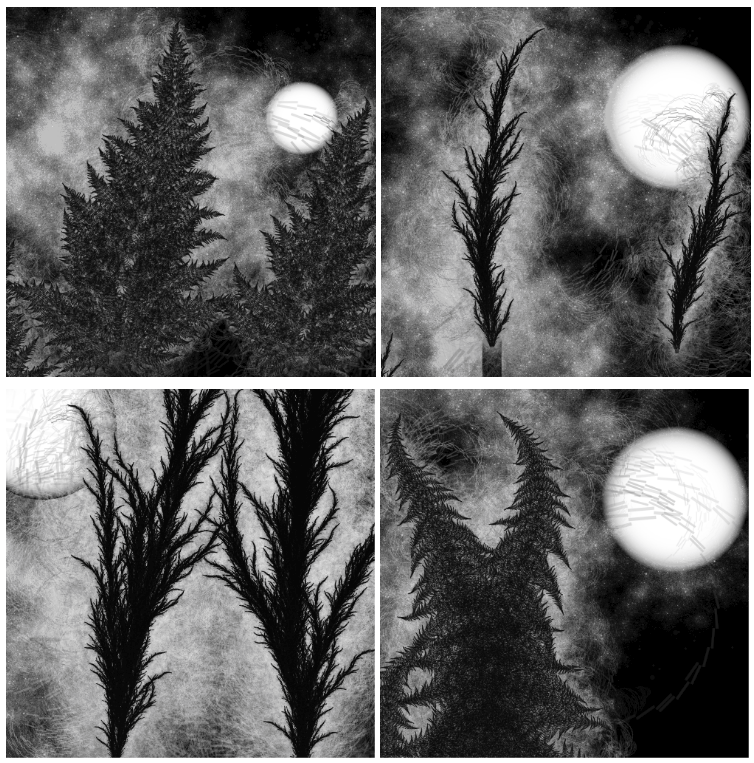
Différents résultats obtenus avec la même grammaire de base, en modifiant le nombre et la taille des arbres, l’angles des feuilles ainsi que la taille et l’emplacement de la lune.
Approches basées sur des automates cellulaires
Les automates cellulaires sont des modèles de calculs discrets basés sur des grilles. Inventés et développés dans les années 50 principalement par John Von Neumann, ils ont principalement été étudiés en informatique théorique, en mathématique ainsi qu’en biologie. Un automate cellulaire est donc basé sur une grille. Le principe est que chaque cellule qui compose la grille peut présenter différents états (par exemple deux états possibles : un état vivant et un état mort). Les états des cellules évoluent en fonction de l’état des cellules voisines à un instant donné. Dans les automates cellulaires, le temps avance de façon discrète, c’est à dire pas à pas. Prenons l’exemple de l’automate cellulaire le plus célèbre : Le jeu de la vie de Conway pour mieux comprendre.
Le jeu de la vie peut être décrit par deux règles simples. A chaque étape, l’état d’une cellule évolue en fonction de l’état de ses huit voisines :
- Si une cellule est morte et qu’elle a exactement trois voisines vivantes, elle passe à l’état vivant.
- Si une cellule est vivante et qu’elle a deux ou trois voisines vivantes elle garde son état, sinon elle passe à l’état mort.
Prenons quelques exemples visuels. Les cellules vivantes sont représentées en noir et les cellules mortes en blanc. Pour chaque exemple, c’est l’état de la cellule du milieu qui nous intéresse.
.png)
Ici la cellule du milieu est morte et elle a seulement deux voisines vivantes, elle ne change donc pas d’état.
.png)
Ici la cellule du milieu est morte et elle a exactement trois voisines vivantes, elle devient donc vivante à son tour.
.png)
Ici la cellule du milieu est vivante et elle a quatres voisines vivantes, elle passe donc à l’état mort.
Les exemples présentés ci-dessus sont très simples puisque l’on s’intéresse seulement à la case du milieu d’une grille de taille très réduite. En général, quand on étudie le comportement des automates cellulaires, on utilise des grilles bien plus grandes. Dans ces grandes grilles, des formes plus complexes peuvent apparaître et évoluer. Par exemple avec les bonnes conditions initiales, il est possible de créer des formes qui se déplacent dans la grille. On appelle ces formes des vaisseaux.


Le plus petit vaisseau possible dans le jeu de la vie (appelé un glider). A droite, son évolution est détaillé lentement.
En considérant des grilles plus grandes et des conditions initiales plus complexes, des structures beaucoup plus importantes peuvent évoluer.

Quand les grilles deviennent trop grandes, en général on ne répresente plus les délimitations entre les cellules pour pouvoir mieux visualiser.
Voici un exemple de vaisseaux beaucoup plus grand qui laisse dans son sillage des objets capables de générer de nouveaux petits vaisseaux en diagonales. On voit bien qu’une grande complexité peut apparaître d’un automate avec des règles très simples (seulement deux règles pour le jeu de la vie).
Il est possible de construire tout un tas de machine dans le jeu la vie et même des ordinateurs fonctionnels (Voir ce lien pour un exemple). Ils sont d’une complexité énorme et extrêmement lents mais ils prouvent qu’il est possible d’obtenir des systèmes très complexes à partir de règles très simples. Tous les éléments d’un ordinateur (la mémoire, l’unité de calcul, le programme etc..) sont construits grâce à différents types d’objets qu’il est possible d’obtenir dans le jeu de la vie. Par exemple, les bits d’informations dans ces ordinateurs sont représentés par des petits vaisseaux. Pour ceux qui souhaitent en apprendre plus sur le jeu de la vie, vous pouvez aller voir cette excellente vidéo.

Exemple de machine créée dans le jeu de la vie (Les couleurs des cellules sont inversées par rapport aux autres examples). Chaque pixel qui se déplace est en fait un petit vaisseau.
Les objets dans le jeu de la vie présentent en général des comportements qui ressemblent à ceux que l’on retrouve dans la nature puisque leur évolution est basée sur des règles simples. Les automates cellulaires ont donc beaucoup servi à modéliser des systèmes environnementaux. C’est donc pour cette raison qu’ils sont intéressants dans le cadre de la génération procédurale de contenu.
Ils ont ainsi été utilisés dans les jeux vidéo pour modéliser de la pluie, du feu, des écoulements de fluides ou encore des explosions. Cependant, ils ont aussi été utilisés pour de la génération de cartes ou de terrain.
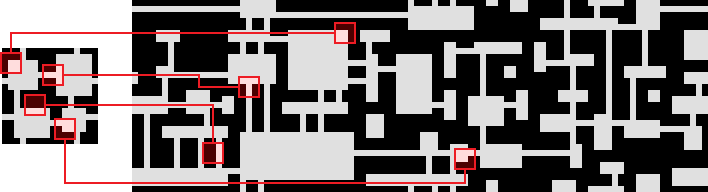
Par exemple, dans un jeu d’exploration de cave en 2 dimensions vu du dessus. Dans ce jeu, chaque salle est représentée par une grille de taille 50*50 cellules. Chaque cellule peut présenter deux états : vide ou roche. L’automate cellulaire est défini par une seule règle d’évolution:
- Une cellule devient ou reste de type roche si au moins 5 de ces voisins sont de type roche, sinon elle devient ou reste vide.
L’état initial est créé aléatoirement, chaque cellule ayant 50% de chance d’être dans l’un des deux états.
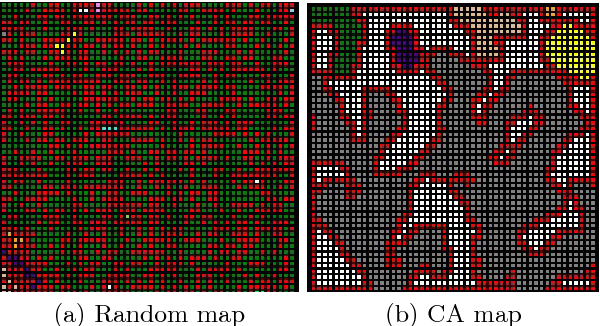
En faisant évoluer la grille depuis son état initial (à gauche) durant plusieurs pas de temps, on obtient un résultat comme sur l’image de droite avec des cases de vides en gris au milieu et des cases de roches en rouge et blanc. Les autres couleurs indiquent des zones de vides qui ne sont pas accessibles car entourées de roche. On remarque que les automates cellulaires permettent de représenter l’érosion.
Pour obtenir des zones plus grandes, on peut générer plusieurs grilles et les regrouper ensuite dans une nouvelle grille plus grande.

9 grilles de taille 50*50 sont générées et mises ensemble. On trace des tunnels là où c’est le plus court s'il n'y a pas de chemin.
En changeant le nombre de cellules à considérer, les règles de l’automate ainsi que le nombre de pas d’évolution on peut obtenir différents types de résultats.
Les automates cellulaires (et les algorithmes constructifs en général) ont l’avantage de présenter un petit nombre de paramètres. Ils sont donc relativement simples à comprendre et implémenter. Cependant, il est difficile de prévoir l’impact sur le résultat final du changement d’un paramètre puisqu’en général les paramètres impactent plusieurs éléments du résultat généré. De plus il n’est pas possible d’ajouter des critères ou des conditions sur le résultat. On ne peut donc pas assurer la jouabilité ou la solvabilité des niveaux générés puisque les caractéristiques de gameplay du jeu sont indépendantes des paramètres de l’algorithme. Il est donc souvent nécessaire d’ajouter une couche de traitements pour corriger les éventuels problèmes. Ainsi dans l’exemple précédent avec l’automate cellulaire il fallait créer des tunnels manuellement si les grilles générées ne présentaient pas de chemin.
Nous allons donc maintenant nous intéresser à des méthodes plus complexes, basées sur de l’Intelligence Artificielle et qui permettent entre autres d’ajouter des conditions et des critères sur les résultats générés.
Approches de génération procédurale avec de l’IA
Maintenant que nous avons vu les principales approches classiques appelées méthodes constructives, intéressons nous aux approches basées sur l’IA. Ces approches peuvent être hybrides et mixer de l’IA avec des méthodes plus classiques comme celles présentées précédemment. La plupart des méthodes présentées dans cette partie ne sont pas encore vraiment implémentées dans des jeux commerciaux mais il semble assez probable qu’elles fassent peu à peu leur apparition puisqu’elles permettent d’aller encore plus loin dans la génération procédurale.
Méthodes basées sur de la recherche
On l’a vu dans les articles précédents, les algorithmes de recherche sont une partie importante de l’IA, on les retrouve donc naturellement dans le domaine de la génération procédurale. Avec cette approche, un algorithme d’optimisation (souvent un algorithme génétique) recherche du contenu répondant à certains critères définis en amont. L’idée est de définir un espace des possibilités qui correspond à l’ensemble du contenu qu’il est possible de générer pour le jeu. On considère qu’une solution satisfaisante existe dans cet espace et l’on va donc le parcourir avec un algorithme afin de trouver ce contenu satisfaisant. Trois composants principaux sont nécessaires pour ce type de génération procédurale :
-
Un algorithme de recherche. C’est le cœur de l’approche. En général un algorithme génétique simple est utilisé mais il est possible d’utiliser des algorithmes plus poussées qui peuvent prendre en compte des contraintes ou se spécialiser sur un type de contenu particulier.
-
Une représentation du contenu. C’est la façon dont le contenu généré sera vu par l’algorithme de recherche. Par exemple pour de la génération de niveau, les niveaux pourraient être représentés sous la forme de vecteurs contenant des informations comme la géographie du niveau, les coordonnées des différents éléments présents dans le niveau ainsi que leur type etc.. Il faut qu’à partir de cette représentation (souvent vectorielle), il soit possible d’obtenir le contenu. L’algorithme de recherche parcourt l’espace des représentations pour trouver le contenu pertinent. Le choix de la représentation impacte donc le type contenu qu’il sera possible de générer ainsi que la complexité de la recherche.
-
Une ou plusieurs fonctions d’évaluation. Il s’agit de modules qui regardent un contenu généré et qui mesurent la qualité de ce contenu. Une fonction d’évaluation peut par exemple mesurer la jouabilité d’un niveau, l’intérêt d’une quête ou encore les qualités esthétiques d’un contenu généré. Trouver de bonnes fonctions d’évaluations est souvent une des tâches les plus difficile lorsque l’on fait de la génération de contenu avec de la recherche.
Les méthodes basées sur la recherche sont sans aucun doute les méthodes les plus versatiles puisque quasiment n’importe quel type de contenu peut être généré. Cependant, elles présentent aussi des défauts, le premier étant la lenteur du processus. En effet, chaque génération de contenu prend du temps puisqu’il faut évaluer un grand nombre de contenus candidats. De plus il est souvent assez difficile de prévoir le temps que mettra l’algorithme pour trouver une solution satisfaisante. Ces méthodes ne sont donc pas vraiment applicables dans les jeux où la génération du contenu doit être faite en temps réel ou très rapidement. De plus pour obtenir de bons résultats il est nécessaire de trouver une bonne combinaison d’un algorithme de recherche, d’une représentation du contenu et d’une façon d’évaluer ce contenu. Cette bonne combinaison peut-être difficile à trouver et nécessiter un travail itératif.
Tout cela étant assez théorique, prenons un exemple. Un des cas d’usage où ce genre d’approche peut être intéressant est la création et l’agencement automatique de pièces. L’idée est d’être capable d’agencer de façon cohérente une pièce à partir d’un certain nombre d’objets spécifiés en amont.

Arranger de façon cohérente et fonctionnelle du mobilier dans une pièce est une tâche complexe, qui doit considérer de nombreux paramètres comme les relations de dépendance entre différents objets, leur relation spatiale par rapport à la pièce etc.. Il est donc nécessaire de trouver une représentation des données qui capture ces différentes relations.
Représentation des données :
Pour chaque objet, on assigne ce que l’on appelle une bounding box, c’est à dire une délimitation en 3 dimensions de l’objet. On assigne aussi pour chaque objet un centre, une orientation, et un sens (par exemple un canapé à une face avant et une face arrière). On considère aussi pour certains objets un cône de vision (par exemple il ne doit pas y avoir d’objets devant une TV, on défini donc un cône de vision devant la TV qui doit être vide). On assigne aussi d’autre paramètres aux objets comme la distance au mur le plus proche, la distance au coin le plus proche, la hauteur, l’espace nécessaire qu’il faut laisser devant l’objet pour qu’il soit fonctionnel etc… Une pièce est donc représentée par l’ensemble des paramètres des différents objets.
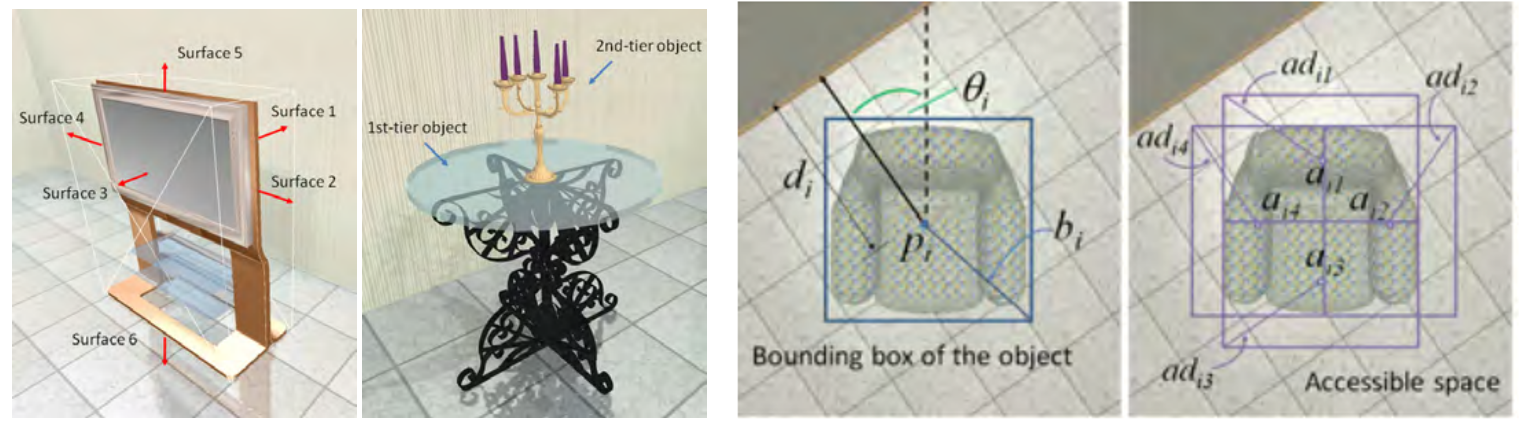
Caractéristiques extraites des objets
Fonction d'évaluation :
Pour savoir si une pièce est cohérente ou non, on a besoin d’une fonction qui regarde la représentation des données d’une pièce et qui retourne un score.
Pour savoir ce qui est une pièce satisfaisante, on utilise un ensemble de pièces aménagées à la main par un humain. On extrait des caractéristiques pertinentes pour le placement des différents objets de la pièce. Ainsi, on observe les relations spatiales entre les différentes objets. Par exemple une TV est toujours contre un mur avec un canapé en face, une lampe est souvent posée sur une table, l’accès à une porte doit être dégagé etc..
Ces différents critères sont utilisés comme référence dans la fonction d’évaluation. Celle-ci mesure l’accessibilité, la visibilité, l’emplacement ainsi que les relations entre tous les objets et regarde si ces valeurs sont cohérentes avec celle des pièces faites par des humains. Plus ces valeurs sont proches des pièces d’exemples plus le score sera bon.
Algorithme de recherche:
L’algorithme de recherche utilisé est l’algorithme du Recuit Simulé qui est un algorithme très simple. Pour commencer la génération, on indique à l’algorithme les différents objets que l’on souhaite mettre dans la pièce et la recherche va permettre de trouver une disposition cohérente de ces objets. On commence avec une disposition aléatoire des objets. A chaque itération de la recherche, une petite modification de la salle est effectuée. L’algorithme autorise différentes modifications d’agencement comme déplacer un objet (rotation et/ou translation) et intervertir l’emplacement de deux objets.
Ensuite, la nouvelle disposition de la salle est évaluée par la fonction d’évaluation. Si la nouvelle disposition est meilleure que la précédente, on la garde. Si par contre elle est moins bonne, on la garde selon une certaine probabilité. Cette probabilité de garder une moins bonne solution s’appelle la température et décroît en général avec le temps. Son intérêt est d’éviter de se retrouver lors de la recherche dans ce qu’on appelle un optimum local, c’est à dire une bonne solution mais pas la meilleure. L’objectif à la fin de la recherche est d’avoir trouvé l’optimum global et donc la meilleure solution.

À gauche l’initialisation aléatoire et à droite le résultat après la recherche
Avec un temps de recherche assez long, cette approche donne des résultats très satisfaisants. D’autres approches plus poussées (comme celle-ci permettent de trouver automatiquement les objets à mettre dans la pièce.
Comme dit précédemment, ce genre d’approches n’est pas encore vraiment mise en place dans des jeux commerciaux, mais on voit tout de suite l’intérêt pour la génération d’environnement. Elles ont aussi par exemple été utilisées pour créer des cartes du jeu Starcraft ou encore dans Galactic arm race pour trouver automatiquement des caractéristiques d’armes qui plaisent au joueur

Carte de Starcraft générée par recherche
D’autres approches de génération procédurales peuvent être combinées à des méthodes de recherche, par exemple les méthodes basées sur des grammaires. En effet, les grammaires étant une représentation du contenu, il est possible de rechercher avec un algorithme plutôt que manuellement les règles et les grammaires les plus adaptées pour générer son contenu.
Méthodes basées sur un solveur
Les méthodes basées sur un solveur sont assez proches de celles basées sur de la recherche puisqu’il s’agit aussi de chercher une solution dans un espace de possibilités, cependant la méthode de recherche est différente. Au lieu de chercher des solutions complètes de plus en plus pertinentes, ces méthodes cherchent d’abord des solutions partielles afin de réduire au fur et à mesure l’espace des possibilités pour trouver au final une solution complète satisfaisante. Ici la recherche est posée comme un problème de satisfaction de contrainte et les méthodes de résolution sont plus spécialisés (on parle de solveurs).
Ainsi à la différence de méthodes comme la MCTS vue dans l’article précédent qui peut s’arrêter n’importe quand et aura toujours une solution (probablement non optimale mais une solution quand même), ces approches ne peuvent pas être arrêtés en milieu de recherche puisqu’elles n’auront alors qu’une solution partielle au problème.
Un exemple simple de problème de satisfaction de contrainte est la résolution d’une grille de sudoku. Les contraintes sont les règles du jeu et l’espace des possibilités correspond à l’ensemble des choix possibles pour les différentes cases. L’algorithme va trouver des solutions partielles qui respectent les contraintes en remplissant au fur et à mesure la grille, réduisant ainsi les possibilités restantes. Il peut arriver avec de genre d’approches d’arriver à une contradiction où il n’est plus possible d’avancer la résolution en respectant les contraintes. Si cela arrive, il faut alors relancer la recherche. En générale les solveurs sont assez poussés pour essayer d’éviter ces problèmes.
Prenons un exemple : l’algorithme Wave Function Collapse. Cette approche est vraiment récente, en effet elle a été proposée en 2016. L’approche peut être implémentée comme un problème de satisfaction de contrainte.
L’idée de base est de générer une grande image en 2 dimensions en se basant sur une plus petite image donnée en entrée. L’image générée a comme contrainte d’être localement similaire à l’image en entrée.
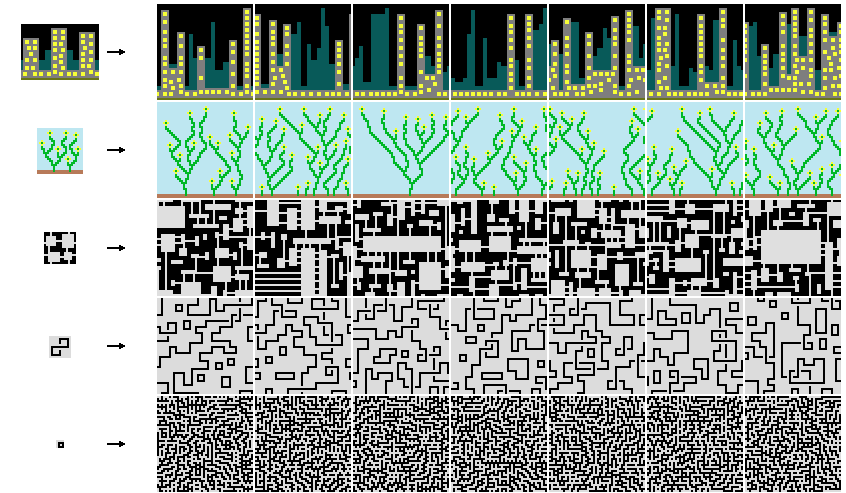
Exemples de résultats présents sur le github. A gauche on peut voir l’image en entrée et à droite différentes générations obtenues
Les contraintes de similarité sont les suivantes :
- Chaque motif d’une certaine taille NN pixel (par exemple 33) qui est présent dans l’image généré doit au moins apparaître une fois dans l’image de base
- La probabilité de trouver un certain motif dans l’image généré doit être le plus possible similaire à sa fréquence de présence dans l’image initiale.
Exemples de résultats présents sur le github. A gauche l’image en entrée et à droite différentes générations obtenues
Au début de la génération, l’image générée est dans un état ou chaque pixel peut prendre n’importe qu’elle valeur (couleur) présente dans l’image en entrée. On peut faire l’analogie avec une grille de sudoku où au début de la résolution une case peut prendre plusieurs valeurs. L’algorithme est le suivant :
- Une zone de taille N*N est choisie dans l’image. Au sudoku on démarre par remplir les cases où il n’y a qu’une seule valeur possible. De façon analogue, ici la zone choisie est celle qui présente le moins de possibilités différentes. Au début de la génération toutes les zones ont les mêmes possibilités puisqu’on démarre depuis zéro. On choisit donc une zone au hasard pour démarrer l’algorithme. La zone choisie est remplacée par un motif de même taille présent dans l’image initiale. On choisit le motif en fonction des fréquences.
- La seconde phase correspond à une propagation de l’information. Comme une zone a été définie, il est probable que les pixels autour de cette zone se retrouvent plus contraints en terme de possibilité. Au sudoku, en remplissant certaines cases, on rajoute des contraintes sur les cases restantes. Ici le principe est le même puisque les motifs possibles sont contraints par l’image de base.
L’algorithme continue ainsi en alternant ces deux phases jusqu’à ce que toutes les zones de l’image générée soient remplacées.

On peut voir ici la façon dont l’algorithme procède pour générer l’image, étape par étape. Chaque pixel est représenté comme la moyenne des couleurs qu’il pourra prendre. Par exemple si un pixel peut-être noir ou blanc, au début il sera représenté en gris.
On peut s’amuser à générer un labyrinthe en se basant sur une image comme celle - ci.


On peut voir ici la façon dont l’algorithme procède pour générer l’image, étape par étape. Chaque pixel est représenté comme la moyenne des couleurs qu’il pourra prendre. Par exemple si un pixel peut-être noir ou blanc, au début il sera représenté en gris.
Petit point terminologie :
En mécanique quantique, un objet peut se retrouver dans plusieurs états en même temps (cf le fameux chat de Schrödinger). On parle de superposition d’états. Cela n’est évidemment pas possible avec les objets en physique classique. Cependant, ces objets qui sont dans une superposition d’états semblent obligatoirement revenir dans un seul des différentes états quand on les observe. Il est ainsi impossible d’observer directement la superposition d’états. On appelle ce phénomène la réduction du paquet d’onde et en anglais Wave Function Collapse. C’est donc ce principe qui a inspiré le concepteur pour le développement de l’algorithme. On retrouve en effet, un petit peu cette idée dans les valeurs possibles que peuvent prendre les différents pixels qui se réduisent au fur et à mesure de l’avancement de l’algorithme.
Une version interactive d’un cas simple de Wave Function Collapse peut être trouvée sur ce site web. Il est excellent pour comprendre intuitivement le fonctionnement et particulièrement comment le choix d’une case impacte les possibilités des cases autours.
Les exemples montrés précédemment appliquent la WFC en 2 dimension, mais il est bien sur possible de la généraliser en 3 dimensions.

2 exemples de terrains générés par Wave Function Collapse
Le github de l’algorithme WFC présente énormément de ressources et d’exemples de ce qu’il est possible de faire avec cet algorithme. L’algorithme étant un problème de satisfaction de contrainte, il est justement possible d’ajouter de nouvelles contraintes (comme avoir forcément la présence d’un chemin par exemple) pour forcer un résultat différent.
L’approche Wave Function Collapse est assez simple à mettre en œuvre et permet d’obtenir de très bons résultats. C’est pourquoi elle a été très rapidement mise en application dans le monde du jeu vidéo indépendant (par exemple dans Bad North sorti très récemment et dans Caves of Qud toujours en early access).
Méthodes de Machine Learning
La génération procédurale basée sur du Machine Learning apprend à modéliser du contenu à partir de données amassées préalablement dans l’optique de générer du nouveau contenu similaire. Les données de contenu qui seront utilisées pour apprendre le modèle peuvent être créés manuellement ou éventuellement extraites d’un jeu déjà existant par exemple. Dans tous les cas, cette étape de construction d’un jeu de données est cruciale et si les données ne sont pas en quantité et en qualité suffisante les résultats seront très certainement mauvais. Dans les approches basées sur la recherche, le résultat attendu est défini assez explicitement (à travers la fonction d’évaluation) et une recherche dans l’espace des possibilités est effectuée pour trouver une solution qui correspond aux critères demandés. Avec le Machine Learning, le contrôle sur le résultat final est moins explicite puisque c’est le modèle de Machine Learning qui va directement générer le contenu. C’est donc surtout le travail sur le jeu de données d’apprentissage qui conditionnera le résultat final.
Dans les jeux commerciaux, cette approche est encore très peu démocratisée, les développeurs optant le plus souvent pour des approches plus simples (comme WFC par exemple). La raison principale est probablement qu’il est assez difficile de construire un jeu de données suffisamment important pour bien modéliser le contenu. Cependant, la recherche dans le domaine est très active et de nombreuses nouvelles méthodes voient régulièrement le jour. Il est probable que dans les années à venir, de plus en plus de jeux se basent sur ces approches pour générer procéduralement leurs univers.
Intéressons-nous donc à quelques possibilités intéressantes offertes par le Machine Learning.
Méthodes de tuiles avec Machine Learning
Les méthode de Machine Learning les plus simple pour la génération procédurale sont probablement les modèles de Markov et plus particulièrement les chaînes de Markov. Les chaînes de Markov sont un ensemble de technique qui apprennent les probabilités d’apparition d’éléments d’une séquence en fonction des éléments précédents de cette séquence. Ces méthodes ont notamment été utilisées dans le monde de la recherche pour générer de nouveaux niveaux dans Super Mario Bros. Pour ce faire, les niveaux du jeu ont été découpés en bandes verticales. Ainsi, un niveau peut être représenté comme une séquence de bandes verticales. La chaîne de Markov va étudier un ensemble de niveaux de Super Mario Bros afin d’apprendre les probabilités de présence d’une certaine bande verticale en connaissant le début du niveau et donc les bandes verticales précédentes.
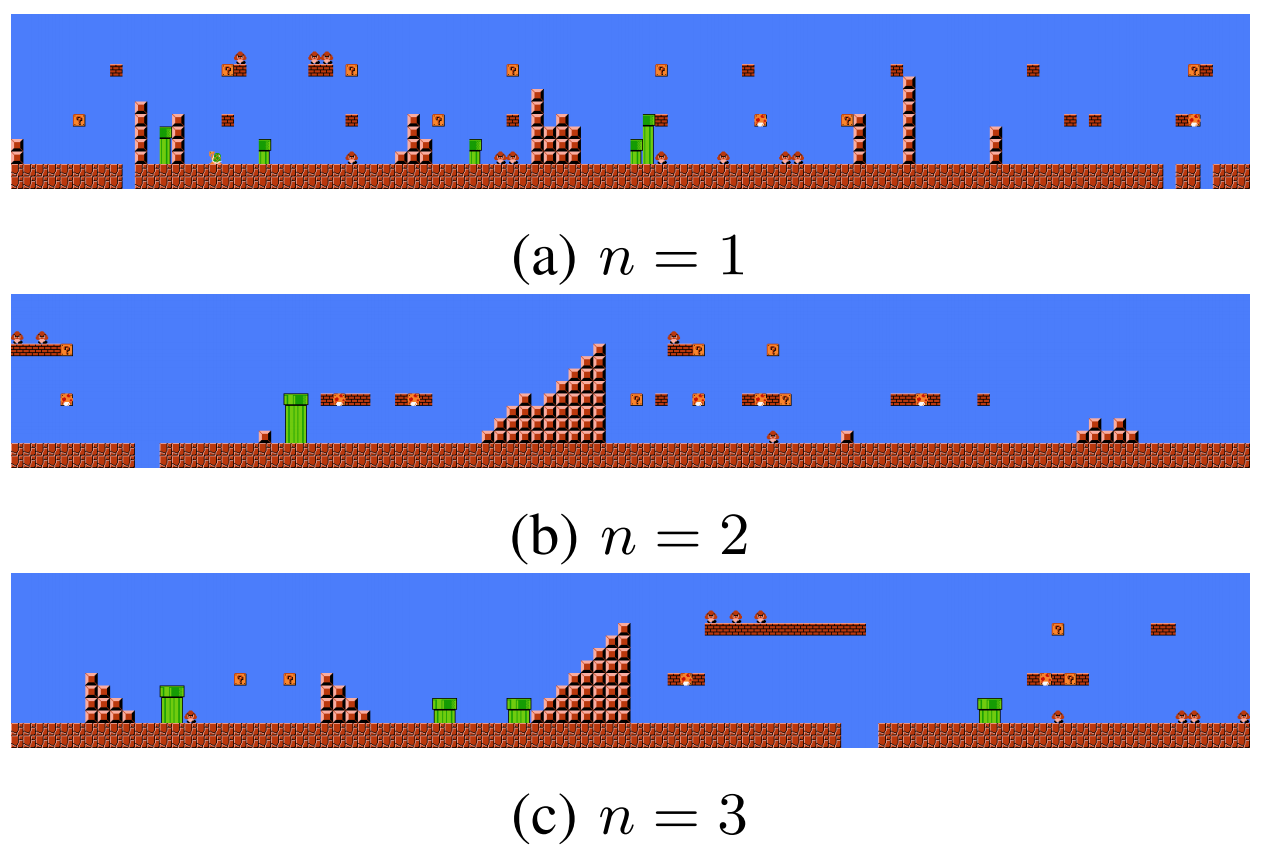
En choisissant une bande verticale aléatoire pour commencer le niveau puis en générant le niveau de gauche à droite bande par bande en fonction des probabilités, il est ainsi possible de générer des niveaux entiers. En général, on calcule les probabilités d’une bande verticale en fonction d’un certain nombre n de bandes précédentes (Si on prend à chaque fois toutes les bandes verticales depuis le début du niveau cela devient très lourd à calculer). En prenant par exemple n=1, chaque bande est seulement conditionnée par la bande précédente. En pratique cela génère des niveau assez différents des niveaux classiques et difficilement finissables. En prenant en considération plus de bandes précédentes (par exemple 2 ou 3), on obtient des niveaux bien plus cohérents et proches de ce qu’on attend d’un niveau de Super Mario Bros. Cette méthode donne d’assez bons résultats surtout en terme de cohérence locale, mais il est évident que sans l’accès à des niveaux existants il n’est pas possible de l’appliquer puisque qu’on ne peut pas calculer les différentes probabilités entre les bandes verticales.
De nombreuses approches mélangeant Machine Learning et tuiles ont été proposés dans le monde de la recherche. Avec ces approches, il devient possible de générer de nouveaux exemples réalistes à partir de quelques exemples seulements.
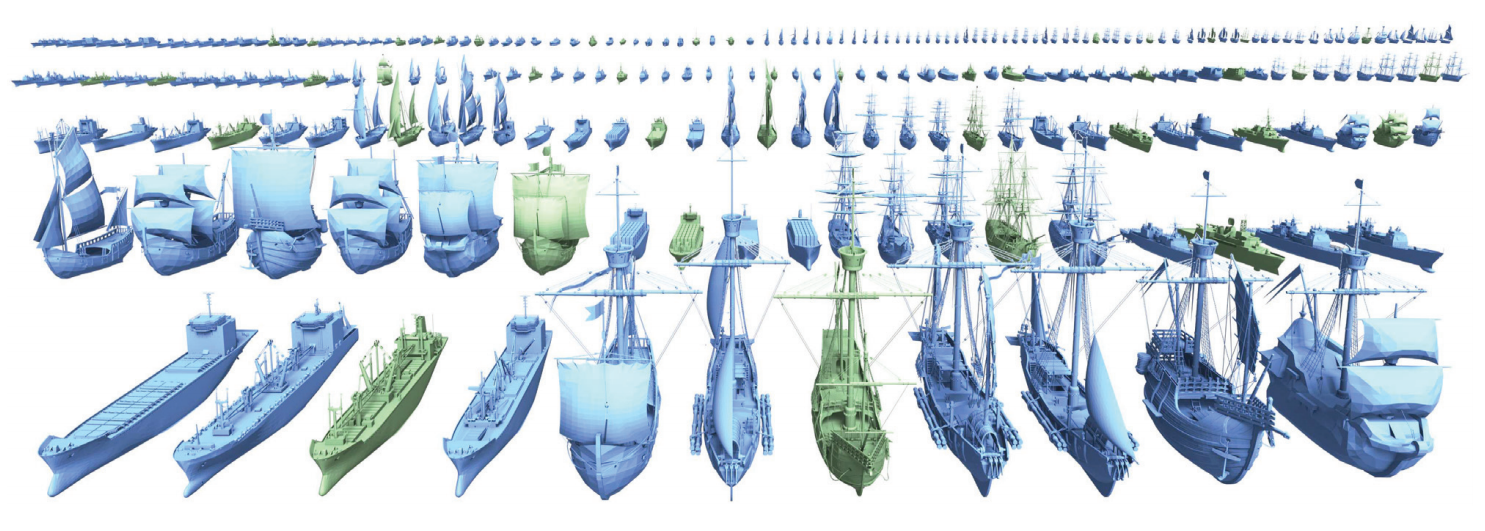
Dans cette image, les bateaux en bleu ont été générés en partie par un modèle de Machine Learning (un modèle Bayésien Hiérarchique) qui a appris à modéliser les relations entre les différentes tuiles des bateaux verts. Voir ici pour plus de détails sur cette approche.
Le Machine Learning dans la génération procédurale est un axe prometteur puisqu’il permet de nouvelles approches, cependant pour obtenir des systèmes qui marchent, il est nécessaire d’avoir des données en quantité suffisante et de trouver comment représenter de façon pertinente ces données. Et quand on parle de représentation des données, en Machine Learning, il semble intéressant de se pencher sur le Deep Learning.
Deep Learning
Le Deep Learning, sous domaine du Machine Learning récemment apparu permet d’étendre les possibilités des modèles classiques dans de nombreux domaines. La génération procédurale en fait partie.
Les Séquences
Le Deep Learning permet de gérer les données qui sont sous la forme de séquence de manière plus performante que les algorithmes classiques grâce à un type de réseaux particuliers que l’on nomme Réseaux de Neurones Récurrents (RNN en anglais). C’est principalement avec ces réseaux que le traitement du texte (NLP en anglais) a été profondément modifié. En effet, les données textuelles sont séquentielles.
Les réseaux récurrents sont assez similaires aux réseaux de neurones classiques à la différence donc qu’ils reçoivent les données en entrée de manière séquentielle plutôt que tout d’un coup. Ainsi, un réseau récurrent appliqué sur du texte recevra les mots d’une phrase un par un dans l’ordre de la phrase. Quand le réseau traite un mot, il a donc en mémoire les informations sur les mots précédents, ce qui peut l’aider pour l’analyse.
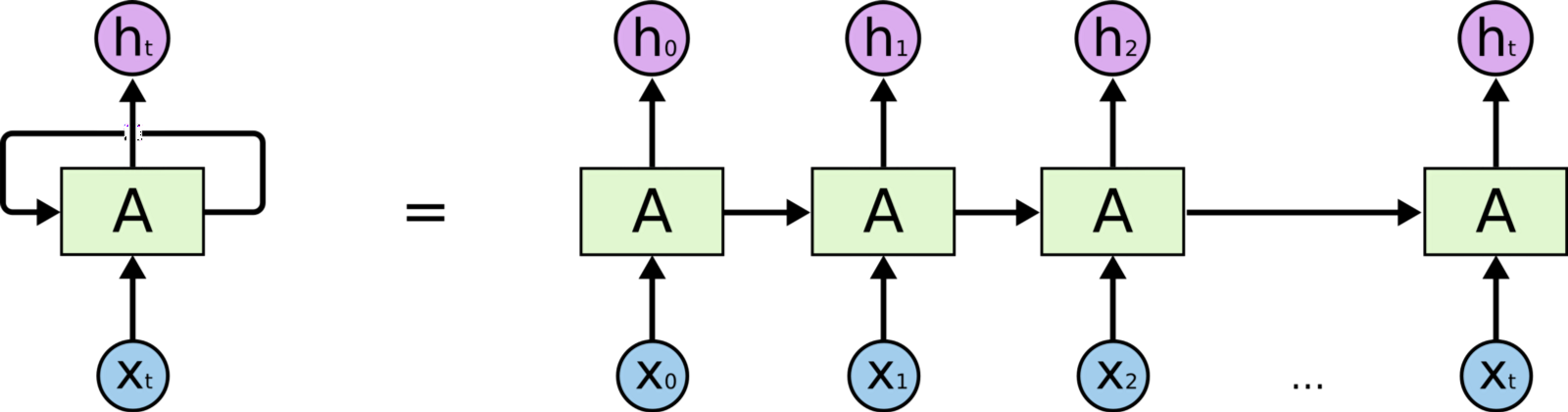
Un réseau récurrent. Les différentes entrées X0, X1 etc.. correspondent aux mots d’une phrase
Cependant les réseaux récurrents classiques sont assez limités en terme de mémoire. Ils ne peuvent pas garder correctement l’information plus de 5 ou 10 pas dans le temps, ce qui n’est en général pas suffisant pour analyser ou générer une phrase complète cohérente (difficile de comprendre si à la fin de la phrase, on a oublié le début). Une variante des réseaux récurrents à été proposée en 1997 : les LSTMs (Long Short Term Memory). Ces réseaux récurrents sont plus compliqués, ils présentent un mécanisme qui permet de déterminer ce qu’il est important de garder en mémoire et ce qui peut être oublié. Grâce à ce mécanisme, les LSTMs repoussent de beaucoup les limites de mémoires des RNNs classiques et sont donc bien plus utilisés.
La génération procédurale de niveau représente parfois les niveaux sous la forme de séquence (pour appliquer des Chaînes de Markov par exemple), il est donc tout à fait possible d’utiliser du Deep Learning de façon similaire afin de générer des niveaux de jeu. Ainsi, en représentant un niveau comme une séquence de tranche verticales et en ayant un jeu de données avec suffisamment de niveaux, il est possible d’apprendre un LSTM à générer une nouvelle séquence de tranches verticales et donc un nouveau niveau de Mario. Les LTSMs à la différence des RNNs classiques et des méthodes plus anciennes comme les Chaînes de Markov permettent de modéliser correctement des séquences assez longues. Cela permet donc d’obtenir des niveaux de Mario avec à la fois une bonne cohérence locale (que l’on obtient déjà avec les méthodes classiques) mais aussi une cohérence globale.
L’un des avantages des réseaux de neurones est qu’ils permettent de représenter les données de différentes façon. Il est donc possible de générer des niveaux de Mario autrement qu’en créant des tranches verticales. En effet, cette méthode présente quelques désavantages, le principal étant qu’il ne sera pas possible de générer un niveau présentant des tranches verticales qui n’étaient pas déjà présentes dans le jeu de données initial. Les niveaux générés risquent donc d’être assez similaires aux niveaux utilisés lors de l’apprentissage.
Une autre approche est donc de représenter un niveau de Mario comme une grille de donnée où chaque élément de la grille correspond à un bloc dans le jeu.

Un niveau de mario représenté comme une grille de différents blocs.
Avec cette représentation, on ne génère plus un niveau tranche par tranche mais bien bloc par bloc. Un niveau de Mario étant en 2 dimensions, il y a plusieurs ordres possible de génération des blocs. On peut déjà générer le niveau horizontalement ou verticalement.
.png)
Génération du niveau horizontale.
La méthode horizontale commencerait par exemple par générer depuis la gauche du niveau la plus haute ligne du ciel (donc avec juste des bloc bleus) puis, une fois arrivée au bord droit du niveau retournerait au début du niveau pour générer la ligne en dessous et ainsi de suite. C’est approche n’est probablement pas la meilleure puisqu’elle rend la cohérence verticale entre différents éléments difficile à assurer. Par exemple si un nuage est présent sur deux lignes verticales, et qu’il a commencé à être généré, il faut s’assurer lors de la génération de la seconde ligne de bien le finir. Cependant, en terme de génération, la fin du nuage arrive longtemps après le début. S’il on considère qu’un niveau de Mario fait 500 blocs de long, le réseau aura générer 500 blocs entre le début et la fin du nuage. Les LSTMs présentent une mémoire améliorée par rapport aux réseaux récurrents classiques mais 500 générations est probablement quand même trop long pour pouvoir assurer de bons résultats dans tous les cas. Une approche de génération verticale semble donc plus pertinente.

Une génération verticale classique à gauche et une génération en serpentant (snaking en anglais) à droite.
Avec cette approche, on génère le niveau colonnes par colonnes. Avec cette génération, il n’y a plus de problème de cohérence verticale puisque les éléments sont générés les uns à la suite des autres. Par contre évidemment, il risque désormais d’y avoir un problème de cohérence horizontale. Cependant, un niveau faisant une quinzaine de blocs verticalement, il est beaucoup plus simple de finir un objet commencé à la colonne précédente puisque seulement une quinzaine de blocs auront été générés entre temps, ce qui est tout à fait dans les cordes de la mémoire des LSTMs. Une autre approche appelée le snaking, génère les blocs en serpentant de haut en bas puis de bas en haut plutôt que de toujours générer du haut vers le bas. Avec le snaking, on diminue encore le nombre de générations entre deux colonnes et donc cela améliore encore un peu plus la cohérence des gros objets comme les rampes.
Avec la génération verticale et le snaking, il est possible de générer de nouveaux niveaux intéressants de Mario en se basant sur un nombre relativement restreint de niveaux déjà existants comme base d’apprentissage (quelques dizaines).
Mario est un jeu en 2 dimensions mais les niveaux sont très linéaires. En général, il suffit d’aller de gauche à droite pour finir le niveau. C’est pourquoi générer un niveau de Mario est une tâche relativement facile. Les jeux d’explorations plus complexes où il faut explorer plusieurs chemins, revenir sur ses pas etc.. (comme les Metroid ou les Castlevania) posent bien plus de difficultés pour la génération. Dès qu’une vraie cohérence en 2 dimensions est nécessaire les approches avec des LSTMs sur des séquences montrent leurs limites. Cependant d’autres approches semblent pouvoir aborder ces problématiques. Par exemple, dans cet article très intéressant une équipe de développement explique les différentes approches qu’ils ont testés afin de réussir à générer des niveaux avec une cohérence en 2 dimensions pour leur jeu Fantasy Raiders.
Deep Dream et Style Transfert
Jusqu’ici, on s’est surtout intéressés aux réseaux récurrents et donc aux données séquentielles, mais le Deep Learning permet aussi de faire des choses jusque-là impossibles dans le domaine de l’image. En effet, les réseaux convolutionnels sont un type de réseaux de neurones présentant des performances exceptionnelles dans les tâches de traitement et de compréhension d’images. Un des premiers exemples vraiment frappant a sans doute été l’algorithme Deep Dream de Google.
La force des réseaux convolutionnels réside dans leur capacité à représenter les données de manière pertinente. Par exemple un réseau de neurones entraîné pour faire de la classification d’image d’animaux, apprend à extraire les caractéristiques importantes des images afin de construire une représentation qui lui permettra de résoudre le problème de classification. Le réseau apprend donc à extraire les caractéristiques communes des chiens, des chats etc..

Deep Dream in the sky
L’idée de l’algorithme Deep Dream de Google est de forcer le réseau à montrer les représentations internes que le réseau a appris. Pour ce faire, on fait fonctionner le réseau à l’envers. On lui donne une image en entrée et on lui demande d’accentuer dans l’image les éléments qu’il reconnaît. Dans l’image du ciel, si une partie d’un nuage ressemble à une tête de chien, le réseau va accentuer cela en montrant à quoi ressemble un chien dans sa représentation interne. En itérant plusieurs fois ce processus sur une même image, on obtient des résultats comme l’image du ciel où le réseau a dessiné des formes partout dans l’image. Le réseau utilisé ayant été entraîné pour reconnaître des animaux et des bâtiments, c’est ce type de formes qu’il a dessinés.
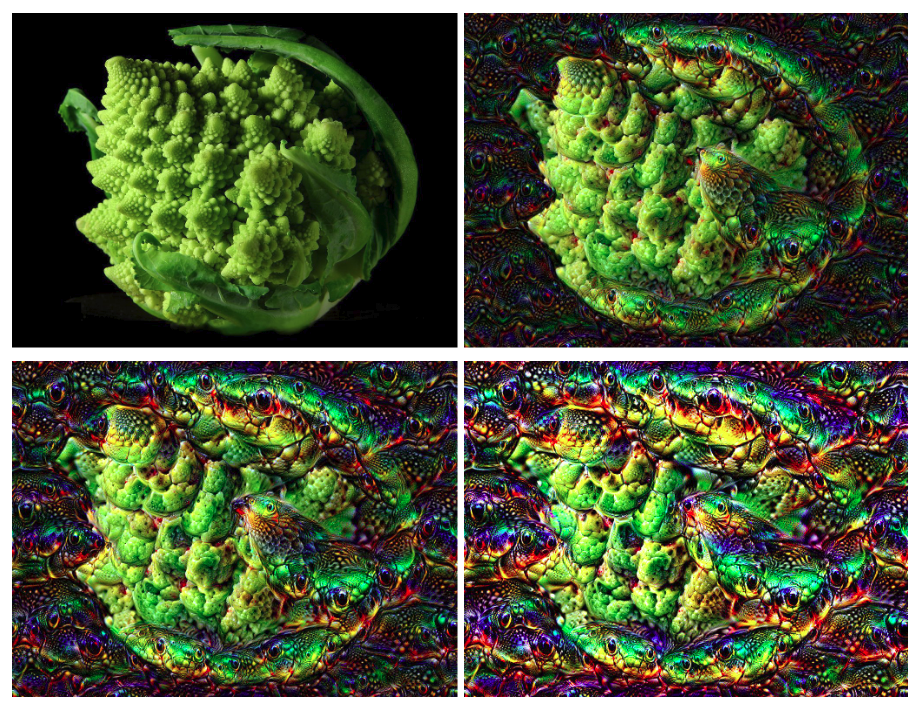
Deep Dream à différents niveaux d’itérations sur notre chou Romanesco. Ici il est un peu plus difficile de voir ce que génère le réseau, mais on peut voir par exemple ce qui semble être une tête d’oiseau apparaître au milieu du chou.
Il est aussi possible de générer complètement une nouvelle image avec Deep Dream en donnant du bruit blanc en entrée. On obtient ainsi des résultats comme l’image ci-dessous où le réseau a généré intégralement ce qui semble être des temples japonais.

Deep Dream sur du bruit blanc
Cette méthode offre des opportunités en génération procédurale, notamment pour générer des textures par exemples, mais surtout elles montrent le potentiel des représentations des données des réseaux convolutionnels et du Deep Learning.
Une autre méthode semble avoir des applications plus directes en génération procédurale : le Style Transfert. Le Style Transfert applique le style d’une image ou d’une œuvre sur une autre image. L’idée est d’utiliser les représentations internes des images qu’un réseau de neurones est capable de construire. En travaillant avec ces représentations, il est possible de rapprocher stylistiquement deux images tout en gardant le plus possible le contenu de l’image initiale.





Voici quelques exemples de Style Transfert en partant de notre image de chou romanesco. Il est aussi possible d’appliquer cette méthode sur des vidéos et donc sur des jeux vidéos (mais pour l’instant assez difficilement en temps réel). Ce lien github présente une galerie de transformations possibles par Style Transfert.
Ces nouvelles approches montrent à quel point les réseaux de neurones sont capables de “comprendre” des images. Cette compréhension en profondeur permet donc une transformation et une création de contenu automatisée qu’il était impossible d’effectuer avant.
C’est pourquoi cela offre de nouvelles opportunités ou de nouvelles façon de travailler dans le cadre de la génération procédurale. Par exemple, le Style Transfert semble pouvoir accélérer le travail des artistes en appliquant un style particulier sur un ensemble de ressources très rapidement. Cet article présente comment un développeur créatif a réussi à appliquer le style d’un film du studio Ghibli (Le Château ambulant) sur un terrain en 3d généré procéduralement.

Le style du studio Ghibli (à gauche) sur un terrain généré procéduralement (à droite)
Pour l’instant, l’utilisation de ces méthodes nécessite encore beaucoup de tâtonnements. Pour pleinement en tirer parti et voir une réelle utilisation dans les jeux vidéo, il faudra probablement trouver des moyens simples et fiables pour collaborer entre l’artiste et l’algorithme, mais à l’heure actuelle ces méthodes sont déjà assez prometteuses.
Les GANs
Les deux approches précédentes sont intéressantes mais lorsque l’on parle de génération et de Deep Learning, c’est un autre type d’architecture en particulier qui sort du lot : Les GANs (Generative Adversarial Networks ou Réseaux Antagonistes Génératifs). Un GAN est une architecture regroupant deux réseaux de neurones antagonistes. En entrée de ces réseaux, on fournit un jeu de données de contenu (souvent des images). Un des deux réseau a pour tâche de générer du contenu similaire à celui du jeu de données en entrée et l’autre réseau doit réussir à distinguer les vrai données de celles générées par le premier réseau. L’apprentissage des deux réseaux est simultané et ils entrent en compétition durant cet apprentissage, ce qu’il leur permet au final de chacun s’améliorer dans leur tâche respective. A la fin de l’apprentissage, on garde seulement le réseau génératif qui est en théorie capable de générer du nouveau contenu très similaire au contenu initial.
Les GANs ont pu être utilisés par exemple pour générer des niveaux du jeu DOOM (1993). Pour ce faire, les chercheurs se sont basés sur plus de mille niveaux du jeu créées par la communauté. Pour chacun des niveaux, ils ont extrait plusieurs images décrivant l’agencement des murs, des plafonds, des objets, des ennemis etc.. Chaque niveau est donc entièrement décrit par 6 images vu du dessus. Le GANs est entraîné sur ces images et à la fin de l’apprentissage est capable de générer de nouvelles images qui sont ensuite transformée en niveaux.

Images décrivant les niveaux, les murs etc.. générées par un GAN. A partir de ces images, il est possible de reconstruire un niveau dans le jeu.
Dans cette vidéo, on peut voir les images générées par le réseau au fur et à mesure de l’apprentissage. Au début, le GANs génère des niveaux informes, puis au fur et à mesure, ils ressemblent de plus en plus à des niveaux générés par l’humain. A la fin de la vidéo, on les voit jouer dans un des niveaux générés.
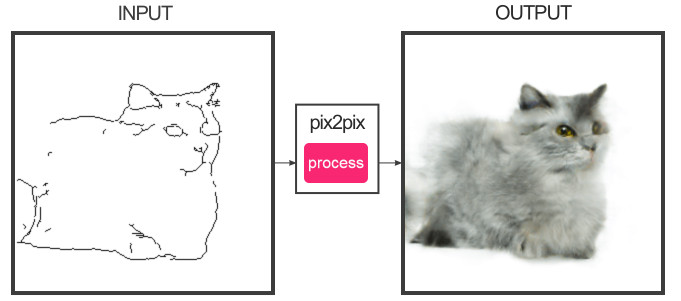
Les GANs ont probablement attiré l’attention du grand public pour la première fois avec l’algorithme pix2pix qui permet de transformer une image. Par exemple, on peut passer d’une image en noir et blanc à sa version colorée, d’une image esquissé à sa version réaliste ou encore d’une image de jour à la même image de nuit.

Résultats obtenus par un GAN avec l’algorithme pix2pix.
Pour pouvoir apprendre ce réseau, il faut déjà disposer d’un jeu de données de paires d’images (par exemple, une paire correspond à une esquisse dessinée et l’image complète correspondante). Durant l’apprentissage, le générateur prend en entrée une esquisse et génère une image complète. Le discriminateur regarde la paire d’images obtenue (l’esquisse et l’image générée) et essaie de déterminer si la paire provient bien du jeu de données initiales ou s’il y a eu génération de l’image. Les deux réseaux s’améliorent au fur et à mesure de l’apprentissage et à la fin, on obtient un générateur capable de transformer n’importe qu’elle esquisse en image. Une des versions de cet algorithme qui a bien plus est Edges2cat qui a été entraînée sur des paires d’images de chat.
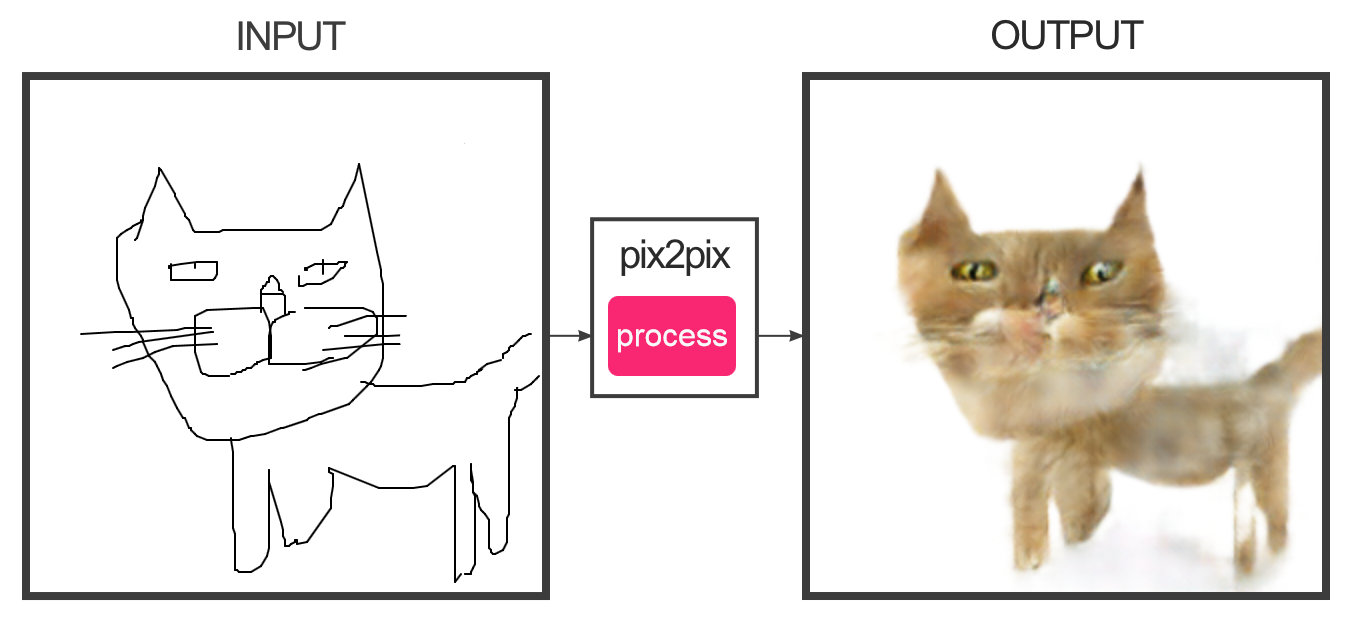
En mettant en entrée une esquisse assez détaillée comme celle du haut, on obtient un résultat photo-réaliste. Quand on est moins talentueux et que l’on donne une esquisse comme celle du bas, les résultats sont moins probants, mais correspondent cependant bien à ce qui est demandé au réseau.
De façon assez étonnante, même en donnant des esquisses qui ne représentent pas du tout des chats, le réseau arrive à s’en sortir et essaie de générer un chat avec la forme demandée.
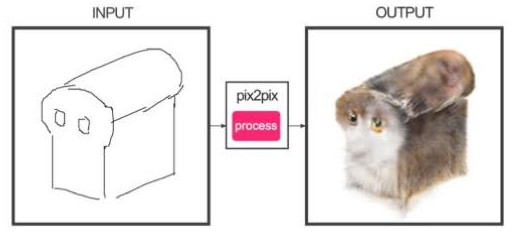

Exemples de résultats obtenus en dessinant des esquisses très différentes du jeu de données initial.
Cette approche a bien sur été utilisée pour faire de la génération procédurale de terrain. On l’a vu précédemment la génération procédurale de terrain passe souvent par du bruit de Perlin ou ses variantes (comme l’uber noise pour No man’s sky) avec des résultats assez inégaux, puisque beaucoup d’ajustement manuel est souvent nécessaire.
Avec une méthode très proche de pix2pix, il est possible d’apprendre un réseau capable de passer d’une esquisse très simple de terrain à un terrain modélisé en 3 dimensions. Il suffit ensuite de travailler sur l’esquisse pour modifier le résultat en 3d, ce qui permet de gagner beaucoup de temps. Dans cette courte vidéo, on voit comment cette méthode est utilisée en temps réel pour générer des terrains réalistes.
Les GANs sont un sujet de recherche assez florissant (la liste des différentes variantes de GANs publiée est assez impressionnante), et leurs cas d’utilisations sont variés. Il est impossible de présenter toutes les initiatives liées aux jeux vidéo, mais en voici une dernière assez intéressante. Se basant sur le CycleGAN (en quelque sorte une version améliorée de pix2pix), cette méthode applique le style graphique d’un jeu dans un autre jeu. Les résultats sont assez impressionnants, cet article donne plus de détails.

Pour finir
Les approches de génération procédurale basées sur l’IA et principalement celles avec du Deep Learning semblent vraiment prometteuses, mais elles ne résolvent clairement pas tous les problèmes. En effet, le Deep Learning est bien adapté aux données naturelles comme des images, du texte ou du son, mais moins aux données avec des contraintes structurelles fortes. Par exemple, les GANs ont encore tendance à générer de temps en temps des images impossibles comme des araignées avec beaucoup trop de pattes ou des balles de tennis-chien.


Quand on veut générer le niveau d’un jeu, ce genre de génération erronée pose problème. En effet, un très beau niveau qui n’est pas finissable n’a que peu d’intérêt. Les problématiques posées par la génération procédurale de contenu dans les jeux vidéo sont donc quelque peu différentes de celles de la génération d’images ou de texte simples et il faut donc adapter les méthodes. Cependant, le travail de recherche sur DOOM a prouvé que c’était possible d’utiliser les GANs pour ce genre de cas d’usage.
Sans être des outils fiables a 100%, il est clair que ces méthodes semblent pouvoir accélérer ou faciliter le travail des développeurs et des artistes. Il est difficile de prévoir si les approches avec du Deep Learning vont remplacer les approches plus classiques, mais il est évident qu’elles apportent de nouvelles perspectives et inspiration sur les méthodes de génération de contenu. Quoi qu’il en soit, il est probable que dans le futur la majeure partie du développement des jeux sera automatisée et les humains s’occuperont des tâches les plus créatives.
Pour ceux intéressés pour aller plus loin, ce github regroupe beaucoup de ressources intéressantes sur la génération procédurale.
Ressources :
Stuart J Russell and Peter Norvig. 2009. Artificial Intelligence: A Modern Approach. Prentice Hall.
http://julian.togelius.com/Togelius2011Searchbased.pdf
http://algorithmicbotany.org/
https://adamsmith.as/papers/wfc_is_constraint_solving_in_the_wild.pdf
http://www.galaxykate.com/pdfs/ComptonMateas-Generative%20Framework%20For%20Generativity.pdf
http://julian.togelius.com/Johnson2010Cellular.pdf
https://people.cs.umass.edu/~kalo/papers/ShapeSynthesis/ShapeSynthesis.pdf
https://dritchie.github.io/pdf/procmod-learn.pdf
https://arxiv.org/pdf/1804.09154.pdf
https://arxiv.org/pdf/1705.02090v2.pdf
https://arxiv.org/pdf/1603.00930.pdf
https://affinelayer.com/pixsrv/
https://www.youtube.com/watch?v=dpYwLny0P8M&t=1878s
https://arxiv.org/pdf/1707.03383.pdf
http://julian.togelius.com/Dahlskog2014Linear.pdf
https://people.cs.umass.edu/~kalo/papers/ShapeSynthesis/ShapeSynthesis.pdf
https://www.redblobgames.com/maps/terrain-from-noise/
http://chrishecker.com/My_Liner_Notes_for_Spore
http://galaxykate0.tumblr.com/post/139774965871/so-you-want-to-build-a-generator
https://github.com/mxgmn/WaveFunctionCollapse
https://www.youtube.com/watch?v=NEscK5RCtlo
https://hal.archives-ouvertes.fr/hal-01583706/file/tog.pdf
https://www.theatlantic.com/technology/archive/2016/02/artificial-universe-no-mans-sky/463308/
http://3dgamedevblog.com/wordpress/?p=836
http://www.escapistmagazine.com/articles/view/video-games/columns/experienced-points/13809-Here-is-How-Fractals-Apply-to-Procedurally-Generated-Games
https://www.youtube.com/watch?v=K0umGtw90Z4
https://www.youtube.com/watch?time_continue=4&v=SePDzis8HqY </p>